本文主要翻译总结自ctsem包帮助文档，帮助文档地址,需要一定R基础，帮助文档非常详细，不懂可以查。

ctsem包简介

可以利用纵向数据构建交叉滞后模型
可以加入随时间/不随时间变化的协变量
可以评估干预的影响
测量间隔可以不一致
可以使用潜变量

安装包

install.packages('ctsem')

本包基于OpenMx构建，为防止报错，运行如下代码，获取最新版本OpenMx

source('http://openmx.psyc.virginia.edu/getOpenMx.R')

注：不更新也能用，但是置信区间跑不出来；更新需要先删掉原来的OpenMx包，不然会报错。

ctsem包Github地址：
https://github.com/cdriveraus/ctsem

数据结构

默认为宽数据，结构（每个个体只有一行记录），长数据可以通过ctLongToWide来转换为宽数据。
读入的应为matrix，而非data。frame。

宽数据示例

dataset

Y1、Y2、Y3为测量变量，在T0、T1、T2三个时间点分别测量；
TD1为随时间变化的自变量；
dT1是T0和T1的时间间隔，dT2是T1和T2的时间间隔；
T11和T12是两个不随时间变化的自变量；

共有两个个体，故有两条记录。

构建模型

examplemodel <- ctModel(n.latent = 2, n.manifest = 2, Tpoints = 3, LAMBDA = diag(2))

n.latent 指定了潜变量的个数
n.manifest 指定了测量变量的个数
Tpoints 指定了测量次数
LAMBDA = diag(2) 测量载荷固定为1.00

指定了如图所示模型：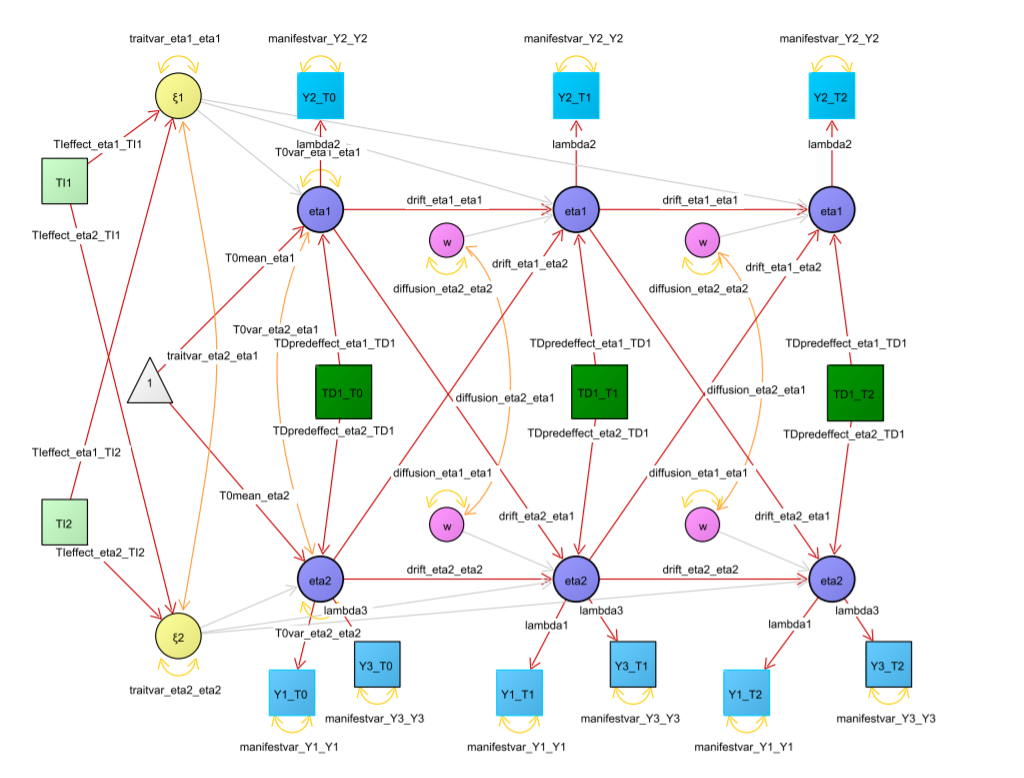
model

案例

采用ctsem包自带的ctExample1数据集，该数据集包括6个时间点Leisure和Happiness的测量数据。

library('ctsem')
data("ctExample1") 
example1model <- ctModel(n.latent = 2, n.manifest = 2, Tpoints = 6, 
    manifestNames = c("LeisureTime", "Happiness"), 
    latentNames = c("LeisureTime", "Happiness"), LAMBDA = diag(2)) 
example1fit <- ctFit(dat = ctExample1, ctmodelobj = example1model)
summary(example1fit, verbose = TRUE)["discreteDRIFTstd"]

得到标化后的回归系数矩阵

$discreteDRIFTstd 
      LeisureTime Happiness 
LeisureTime 0.9728      -0.0499 
Happiness   -0.0138      0.9146

根据该结果我们可以得出leisure的变化happiness的变化持续更久（自回归系数更大，0.97>0.91），即happiness更稳定，更有可能是原因。交叉回归系数-0.04表示随着happiness增加，会导致leisure随之减少。

模型比较

将 drift LeisureTime Happiness固定为0，构建新模型。

testmodel <- example1model 
testmodel$DRIFT[1, 2] <- 0 
testfit <- ctFit(dat = ctExample1, ctmodelobj = testmodel)

和之前的模型进行对比：

mxCompare(example1fit$mxobj, testfit$mxobj)

输出结果

  base comparison ep minus2LL df AIC diffLL diffdf p 
1 ctsem <NA> 16 4177 1184 1809 NA NA NA 
2 ctsem ctsem 15 4197 1185 1827 19.9 1 0.00000833

可以看出模型2和模型1有显著差异，也就是说happiness对leisure time的影响非常重要。

输出置信区间

example1cifit <- ctCI(example1fit, confidenceintervals = "DRIFT")
summary(example1cifit)$omxsummary$CI

输出结果，如果置信区间不包含0，和上面的假设检验等价。

                    lbound estimate ubound note 
drift_LeisureTime_LeisureTime -0.0468 -0.0280 -0.0125
drift_LeisureTime_Happiness -0.1083 -0.0697 -0.0377 
drift_Happiness_LeisureTime -0.0312 -0.0111 0.0087
drift_Happiness_Happiness -0.1486 -0.0896 -0.0459

绘图

data("ctExample1") 
traitmodel <- ctModel(n.manifest = 2, n.latent = 2, Tpoints = 6, LAMBDA = diag(2), 
                      manifestNames = c("LeisureTime", "Happiness"), 
                      latentNames = c("LeisureTime", "Happiness"), TRAITVAR = "auto") 
traitfit <- ctFit(dat = ctExample1, ctmodelobj = traitmodel)
par(mfrow=c(2,2))
plot(traitfit)

加入协变量

不随时间改变的变量

data("ctExample1TIpred") 
tipredmodel <- ctModel(n.manifest = 2, n.latent = 2, n.TIpred = 1, 
                       manifestNames = c("LeisureTime", "Happiness"), 
                       latentNames = c("LeisureTime", "Happiness"), 
                       TIpredNames = "NumFriends", Tpoints = 6, LAMBDA = diag(2), 
                       TRAITVAR = "auto") 
tipredfit <- ctFit(dat = ctExample1TIpred, ctmodelobj = tipredmodel)
summary(tipredfit, verbose = TRUE)["TIPREDEFFECT"] 
summary(tipredfit, verbose = TRUE)["discreteTIPREDEFFECT"] 
summary(tipredfit, verbose = TRUE)["asymTIPREDEFFECT"] 
summary(tipredfit, verbose = TRUE)["addedTIPREDVAR"] # 加入协变量调整后的回归系数

TIpredNames指的是不随时间改变的变量的名称

随时间改变的变量

在某个时间点突然出现的变量（干预、突发事件）可能会对结局产生影响。
影响可能分为两种(短期效应、长期效应)：
假设在某个时间点（T5），对全体个体施加了金钱奖励，干预因素MoneyInt
int

短期效应

data("ctExample2") 
tdpredmodel <- ctModel(n.manifest = 2, n.latent = 2, n.TDpred = 1, Tpoints = 8, 
                       manifestNames = c("LeisureTime", "Happiness"), 
                       TDpredNames = "MoneyInt", 
                       latentNames = c("LeisureTime", "Happiness"), 
                       LAMBDA = diag(2), TRAITVAR = "auto") 
tdpredfit <- ctFit(dat = ctExample2, ctmodelobj = tdpredmodel, 
                   stationary=c('T0VAR','T0TRAITEFFECT')) 
summary(tdpredfit, verbose = TRUE)["TDPREDEFFECT"]

输出的结果为(对最近一次的改变的效应)：

$TDPREDEFFECT
               MoneyInt
LeisureTime           0
Happiness             0
MoneyIntLatent        1

长期效应

data("ctExample2") 
head(ctExample2)
tdpredlevelmodel <- ctModel(n.manifest = 2, n.latent = 3, n.TDpred = 1, 
                            Tpoints = 8, manifestNames = c("LeisureTime", "Happiness"), 
                            TDpredNames = "MoneyInt", 
                            latentNames = c("LeisureTime", "Happiness", "MoneyIntLatent"), 
                            LAMBDA = matrix(c(1,0, 0,1, 0,0), ncol = 3), TRAITVAR = "auto")

tdpredlevelmodel$TRAITVAR[3, ] <- 0 
tdpredlevelmodel$TRAITVAR[, 3] <- 0 
tdpredlevelmodel$DIFFUSION[, 3] <- 0 
tdpredlevelmodel$DIFFUSION[3, ] <- 0 
tdpredlevelmodel$T0VAR[3, ] <- 0 
tdpredlevelmodel$T0VAR[, 3] <- 0 
tdpredlevelmodel$CINT[3] <- 0 
tdpredlevelmodel$T0MEANS[3] <- 0 
tdpredlevelmodel$TDPREDEFFECT[1:3, ] <- c(0,0,1) 
tdpredlevelmodel$DRIFT[3, ] <- c(0,0,-.000001)
tdpredlevelfit <- ctFit(dat = ctExample2,ctmodelobj = tdpredlevelmodel, 
                        stationary=c('T0VAR','T0TRAITEFFECT'))
summary(tdpredlevelfit, verbose = TRUE)[c("DRIFT","TDPREDEFFECT")]

输出的结果为长期效应(对所有改变的效应，见最后一列)：

$DRIFT
               LeisureTime   Happiness MoneyIntLatent
LeisureTime    -0.14211961 -0.21799949      0.5620140
Happiness       0.08478178 -0.01669936     -0.3480144
MoneyIntLatent  0.00000000  0.00000000     -0.0000010

分组分析

data("ctExample4")
basemodel <- ctModel(n.latent = 1, n.manifest = 3, Tpoints = 20, 
                     LAMBDA = matrix(c(1, "lambda2", "lambda3"), nrow = 3, ncol = 1))
freemodel <- basemodel 
freemodel$LAMBDA[3, 1] <- "groupfree" 
groups <- paste0("g", rep(1:2, each = 10))
multif <- ctMultigroupFit(dat = ctExample4, groupings = groups, 
                          ctmodelobj = basemodel, freemodel = freemodel)
summary(multif)

在结果里找到g1_lambda3和g1_lambda3即可。
可以通过之前模型比较的方法进行检验。

ctsem包还可以处理时间序列模型，高阶模型等。有非常好的延伸性。