放假了，全统计系可能只有我一个人还在接统计咨询……

大概他们都不用看演唱会，所以没有为钱所困吧……悲伤……

前言

临床上一类文章的套路是 PSM（倾向性评分匹配）- OS/RFS生存分析 - COX回归，通过这种方式比较两种手术方式/治疗方式的好坏。今天接到的统计咨询也是要写一篇这样的文章，但是他提供了一个样图:

pr1

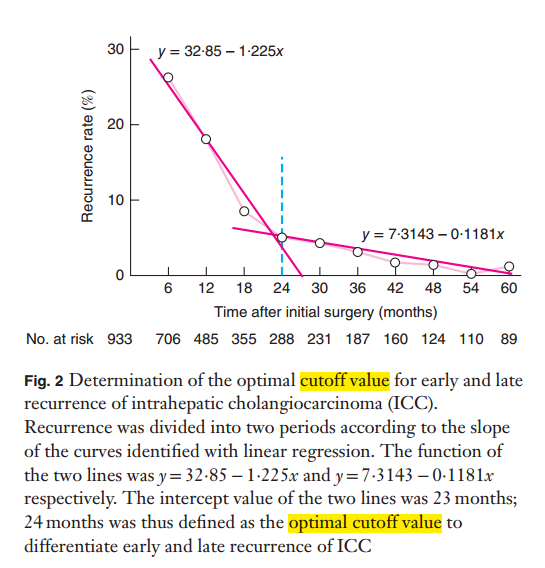
一篇文献中通过绘制该图寻找早期复发与晚期复发的交界点，但是文中并没有具体的做法。

刚看到觉得，嗯，就是分段函数，应该很好做吧，结果做完感觉天都黑了……所以赶紧记录下来。

前期准备

载入包

分段函数的英文是piecewise linear regression，用这个英文加上R去Bing搜索，就可以找到问题的解决方案。

解决方案就是segmented这个包，这个包的描述是:

Given a regression model, segmented “updates” the model by adding one or more segmented (i.e., piece-wise linear) relationships. Several variables with multiple breakpoints are allowed.

就决定是你了！

# load package
library(tidyverse) 
library(segmented)

读入文件

我们读入原始数据，包含每个人的复发距离手术的时间。

# read
a <- read.csv('recur.csv',header=F)

数据预处理

我们按照区间长度为3，将数据整理成【复发时间】【复发人数】的格式。

# assign month
# 整理区间
a$V3 <- ((a$V2-1)%/%3+1)*3

# assign recurence rate
# 计数
b <- a %>% group_by(V3) %>% count(V3)

# 计算复发率
# total为总人数
b$freq <- b$n/total*100

散点图绘制

绘制常规散点图

# 指定x，y
y <- b$freq
x <- b$V3

# 指定回归模型
lin.mod <- lm(y~x)

# 绘图
plot(x,y, pch=1, cex=1.5, #指定点的类型为圆圈，大小1.5
ylim=c(0,60), #纵轴高度
xlab = 'Time after initial surgery(months)', #横轴标签
ylab = 'Recurrence(%)' , #纵轴标签
bty = 'l') #只画纵轴与横轴

分段回归直线拟合

在拟合分段回归直线前，需要人为指定Breaking-point，之后程序会根据拟合的直线重新估计，point可以是一个点，多个point可以用psi=list(c(x1,x2))指定。

# 指定point
segmented.mod <- segmented(lin.mod, seg.Z = ~x, psi=9)

# 拟合分段回归直线
plot(segmented.mod, col='pink', lwd= 2.5 ,add=T)

拟合之后我们需要得到拟合出的回归直线的基本信息,方法也很简单，使用我们常用summary()就可以得到截断点Breaking point（即我们需要求的分界点），同时可以输出部分截距和斜率信息，不过这个不完全。
所以我们可以通过intercept()以及slope()分别求得各段直线的结局与斜率。

# 
summary(segmented.mod)
intercept(segmented.mod)
slope(segmented.mod)

画出截断直线、标注回归方程

根据我们上述得到的信息，我们可以标出截断直线，以及各段的回归方程

abline(v=bp1 lty=2,col='blue') # bp1:截断点的值
text(10, 40, 'y = a1+b1x') # a1,b1：分段1的截距、斜率
text(20, 10, 'y = a2+b2x') # a2,b2：分段1的截距、斜率

最终我们得到这样的图，也得到了交界点，临床上来说，我们找到了早期复发与晚期复发的分界点。

pr2

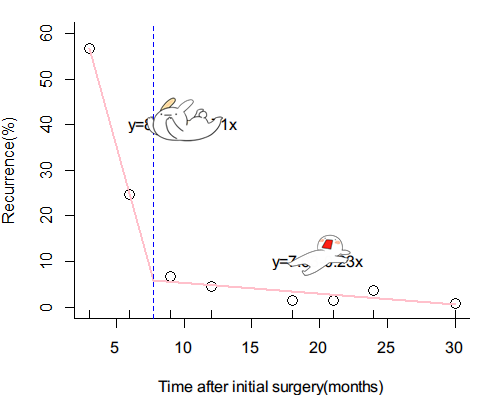
大功告成！
（我喜欢我的马赛克！）

R语言分段线性回归直线拟合与绘图

前言